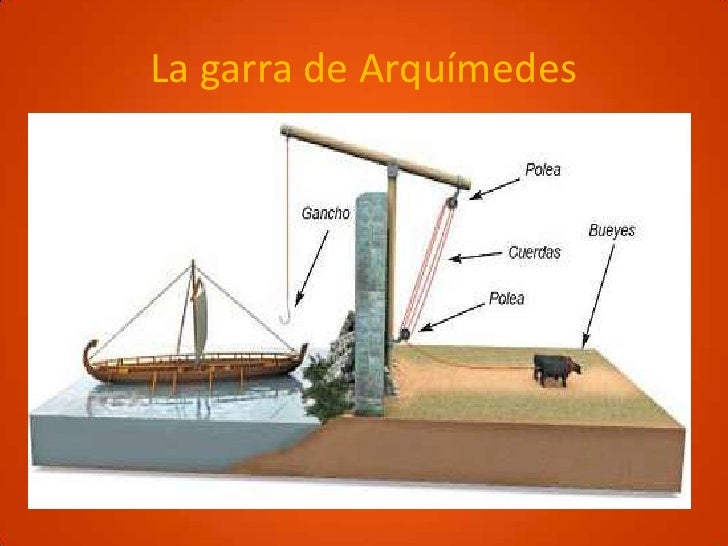
La garra de Arquímedes

Polibio narra que la intervención de Arquímedes en el ataque romano a Siracusa fue decisiva, hasta el punto de que desbarató la esperanza romana de tomar la ciudad por asalto, teniendo que modificar su estrategia y pasar al asedio de larga duración, situación que duró ocho meses, hasta la caída definitiva de la ciudad. Entre los ingenios de que se valió para tal hazaña (catapultas, escorpiones y grúas) se encuentra una que es de su invención: la llamada manus ferrea. Los romanos acercaban todo lo que podían los barcos al muro para enganchar sus escaleras a las fortificaciones y poder acceder con sus tropas a las almenas. Entonces entraba en acción la garra, que consistía en un brazo semejante a una grúa del cual pendía un enorme gancho de metal. Cuando se dejaba caer la garra sobre un barco enemigo el brazo se balancearía en sentido ascendente, levantando la proa del barco fuera del agua y provocando un ingreso del agua por lapopa. Esto inutilizaba los ingenios enemigos y causaba confusión, pero no era lo único que hacía: mediante un sistema de polea y cadenas, dejaba caer súbitamente el barco provocando una escoración que podía llevarlo al vuelco y al hundimiento.^13 15 36 Ha habido experimentos modernos con la finalidad de probar la viabilidad de la garra, y en un documental del año 2005 titulado Superarmas del mundo antiguo (Superweapons of the Ancient World) se construyó una versión de la garra y se concluyó que era un dispositivo factible.

El Siracusia y el tornillo de Arquímedes

Una gran parte del trabajo de Arquímedes en el campo de la ingeniería surgió para satisfacer las necesidades de su ciudad natal, Siracusa. El escritor griego Ateneo deNáucratis cuenta que Hierón II le encargó a Arquímedes el diseño de un enorme barco, el Siracusia, que construyó Arquias de Corinto bajo su supervisión.³² El barco podía ser usado para viajes lujosos, cargar suministros y como barco de guerra. Finalmente su nombre fue cambiado por el de Alejandría, cuando fue enviado como regalo, junto a un cargamento de grano, al rey Ptolomeo III de Egipto.

Se dice que el Siracusia fue el barco más grande de la antigüedad clásica.³³ Según Ateneo, era capaz de cargar 600 personas e incluía entre sus instalaciones jardines decorativos, un gimnasio y un templo dedicado a la diosa Afrodita. Debido a que un barco de esta envergadura dejaría pasar grandes cantidades de agua a través del casco, el tornillo de Arquímedes supuestamente fue inventado a fin de extraer el agua de la sentina. La máquina de Arquímedes era un mecanismo con una hoja con forma de tornillo dentro de un cilindro. Se hacía girar a mano, y también podía utilizarse para transferir agua desde masas de aguas bajas a canales de irrigación. De hecho, el tornillo de Arquímedes sigue usándose hoy en día para bombear líquidos y sólidos semifluidos, como carbón, hielo y cereales. El tornillo de Arquímedes, tal como lo describió Marco Vitruvio en los tiempos de Roma, puede haber sido una mejora del tornillo de bombeo que fue usado para irrigar los jardines colgantes de Babilonia.

La corona dorada

Una de las anécdotas más conocidas sobre Arquímedes cuenta cómo inventó un método para determinar el volumen de un objeto con una forma irregular. De acuerdo conVitruvio, Hierón II ordenó la fabricación de una nueva corona con forma de corona triunfal, y le pidió a Arquímedes determinar si la corona estaba hecha solo de oro o si, por el contrario, un orfebre deshonesto le había agregado plata en su realización.²⁵ Arquímedes tenía que resolver el problema sin dañar la corona, así que no podía fundirla y convertirla en un cuerpo regular para calcular su masa y volumen, a partir de ahí, su densidad. Mientras tomaba un baño, notó que el nivel de agua subía en la bañera cuando entraba, y así se dio cuenta de que ese efecto podría ser usado para determinar el volumen de la corona. Debido a que el agua no se puede comprimir,²⁶ la corona, al ser sumergida, desplazaría una cantidad de agua igual a su propio volumen. Al dividir el peso de la corona por el volumen de agua desplazada se podría obtener la densidad de la corona. La densidad de la corona sería menor que la densidad del oro si otros metales menos densos le hubieran sido añadidos. Cuando Arquímedes, durante el baño, se dio cuenta del descubrimiento, se dice que salió corriendo desnudo por las calles, y que estaba tan emocionado por su hallazgo que olvidó vestirse. Según el relato, en la calle gritaba "¡Eureka!" (en griego antiguo: "εὕρηκα" que significa "¡Lo he encontrado!")²⁷

Sin embargo, la historia de la corona dorada no aparece en los trabajos conocidos de Arquímedes. Además, se ha dudado que el método que describe la historia fuera factible, debido a que habría requerido un nivel de exactitud extremo para medir el volumen de agua desplazada.²⁸

En lugar de esto, Arquímedes podría haber buscado una solución en la que aplicaba el principio de la hidrostática conocido como el principio de Arquímedes, descrito en su tratado Sobre los cuerpos flotantes. Este principio plantea que todo cuerpo sumergido en un fluido experimenta un empuje de abajo hacia arriba igual al peso del fluido desalojado.²⁹ Usando este principio, habría sido posible comparar la densidad de la corona dorada con la de oro puro al usar una balanza. Situando en un lado de la balanza la corona objeto de la investigación y en el otro una muestra de oro puro del mismo peso, se procedería a sumergir la balanza en el agua; si la corona tuviese menos densidad que el oro, desplazaría más agua debido a su mayor volumen y experimentaría un mayor empuje que la muestra de oro. Esta diferencia de flotabilidad inclinaría la balanza como corresponde. Galileo creía que este método era "probablemente el mismo que usó Arquímedes, debido a que, además de ser muy exacto, se basa en demostraciones descubiertas por el propio Arquímedes."³⁰Alrededor del año 1586, Galileo Galilei inventó una balanza hidrostática para pesar metales en aire y agua que aparentemente estaría inspirada en la obra de Arquímedes.

Biografía

Hay pocos datos fiables sobre la vida de Arquímedes. Sin embargo, todas las fuentes coinciden en que era natural de Siracusa y que murió durante el desenlace del sitio de Siracusa. Arquímedes nació c. 287 a. C. en el puerto marítimo deSiracusa (Sicilia, Italia), ciudad que en aquel tiempo era una colonia de la Magna Grecia. Conociendo la fecha de su muerte, la aproximada fecha de nacimiento está basada en una afirmación del historiador bizantino Juan Tzetzes, que afirmó⁷ que Arquímedes vivió hasta la edad de 75 años.⁸ Según una hipótesis de lectura basada en un pasaje corrupto de El contador de arena -cuyo título en griego es ψαμμίτης (Psammites)-, Arquímedes menciona el nombre de su padre, Fidias, unastrónomo.⁹

Plutarco escribió en su obra Vidas paralelas (Vida de Marcelo, 14, 7) que Arquímedes estaba emparentado con el tirano Hierón II de Siracusa.¹⁰ Se sabe que un amigo de Arquímedes, Heráclides, escribió una biografía sobre él pero este libro no se conserva, perdiéndose así los detalles de su vida.¹¹ Se desconoce, por ejemplo, si alguna vez se casó o tuvo hijos.

Entre los pocos datos ciertos sobre su vida, Diodoro Sículo nos aporta uno¹² según el cual es posible que Arquímedes, durante su juventud, estudiase en Alejandría, en Egipto. El hecho de que Arquímedes se refiera en sus obras a científicos cuya actividad se desarrollaba en esa ciudad, abona la hipótesis: de hecho, Arquímedes se refiere a Conon de Samoscomo su amigo en Sobre la esfera y el cilindro, y dos de sus trabajos (El Método de los Teoremas Mecánicos y elProblema del Ganado) están dedicados a Eratóstenes de Cirene.^{Nota 1}

Arquímedes murió c. 212 a. C. durante la Segunda Guerra Púnica, cuando las fuerzas romanas al mando del generalMarco Claudio Marcelo capturaron la ciudad de Siracusa después de un asedio de dos años de duración. Arquímedes se distinguió especialmente durante el sitio de Siracusa, en el que desarrolló armas para la defensa de la ciudad. Polibio,¹³Plutarco,¹⁴ y Tito Livio¹⁵ describen, precisamente, su labor en la defensa de la ciudad como ingeniero, desarrollando piezas de artillería y otros artefactos capaces de mantener a raya al enemigo. Plutarco, en sus relatos, llega a decir que los romanos se encontraban tan nerviosos con los inventos de Arquímedes que la aparición de cualquier viga o polea en las murallas de la ciudad era suficiente como para provocar el pánico entre los sitiadores.¹⁶

Cicerón y los magistrados descubriendo la tumba de Arquímedes en Siracusa, deBenjamin West (1797). Colección privada.

Arquímedes fue asesinado al final del asedio por un soldado romano, contraviniendo las órdenes del general romano, Marcelo, de respetar la vida del gran matemático griego.^17 18 Existen diversas versiones de la muerte de Arquímedes: Plutarco, en su relato, nos da hasta tres versiones diferentes. De acuerdo con su relato más popular, Arquímedes estaba contemplando un diagrama matemático cuando la ciudad fue tomada. Un soldado romano le ordenó ir a encontrarse con el General, pero Arquímedes hizo caso omiso a esto, diciendo que tenía que resolver antes el problema. El soldado, enfurecido ante la respuesta, mató a Arquímedes con su espada. Sin embargo, Plutarco también brinda otros dos relatos menos conocidos de la muerte de Arquímedes, el primero de los cuales sugiere que podría haber sido asesinado mientras intentaba rendirse ante un soldado romano, y mientras le pedía más tiempo para poder resolver un problema en el que estaba trabajando. De acuerdo con la tercera historia, Arquímedes portaba instrumentos matemáticos, y fue asesinado porque el soldado pensó que eran objetos valiosos. Tito Livio, por su parte, se limita a decir que Arquímedes estaba inclinado sobre unos dibujos que había trazado en el suelo cuando un soldado que desconocía quién era, le mató. En cualquier caso, según todos los relatos, el general Marcelo se mostró furioso ante la muerte de Arquímedes, debido a que lo consideraba un valioso activo científico, y había ordenado previamente que no fuera herido.¹⁹

Una esfera tiene 2/3 exactos del volumen y de la superficie del cilindro que la circunscribe. Una esfera y uncilindro fueron colocados encima de la tumba de Arquímedes, cumpliendo con su voluntad.

Las últimas palabras atribuidas a Arquímedes fueron "No molestes mis círculos", en referencia a los círculos en el dibujo matemático que supuestamente estaba estudiando cuando lo interrumpió el soldado romano. La frase es a menudo citada en latín como "Noli turbare circulos meos", pero no hay evidencia de que Arquímedes pronunciara esas palabras y no aparecen en los relatos de Plutarco.²⁰

Cicerón describe la tumba de Arquímedes, que habría visitado, e indica que sobre ella se había colocado una esfera inscrita dentro de un cilindro.²¹ Arquímedes había probado que el volumen y el área de la esfera son dos tercios de los del cilindro que la inscribe, incluyendo sus bases, lo cual se consideró el más grande de sus descubrimientos matemáticos. En el año 75 a. C., 137 años después de su muerte, el orador romano Cicerón estaba sirviendo como cuestor en Sicilia y escuchó historias acerca de la tumba de Arquímedes, pero ninguno de los locales fue capaz de decirle dónde se encontraba exactamente. Finalmente, encontró la tumba cerca de la puerta de Agrigento en Siracusa, en una condición descuidada y poblada de arbustos. Cicerón limpió la tumba, y así fue capaz de ver la talla y leer algunos de los versos que se habían escrito en ella.²²

Los relatos sobre Arquímedes fueron escritos por los historiadores de la antigua Roma mucho tiempo después de su muerte. El relato de Polibio sobre el asedio a Siracusa en su obra Historias (libro VIII) fue escrito alrededor de setenta años después de la muerte de Arquímedes, y fue usado como fuente de información por Plutarco y Tito Livio. Este relato ofrece poca información sobre Arquímedes como persona, y se enfoca en las máquinas de guerra que se decía que había construido para defender la ciudad.

La garra de Arquímedes

Polibio narra que la intervención de Arquímedes en el ataque romano a Siracusa fue decisiva, hasta el punto de que desbarató la esperanza romana de tomar la ciudad por asalto, teniendo que modificar su estrategia y pasar al asedio de larga duración, situación que duró ocho meses, hasta la caída definitiva de la ciudad. Entre los ingenios de que se valió para tal hazaña (catapultas, escorpiones y grúas) se encuentra una que es de su invención: la llamada manus ferrea. Los romanos acercaban todo lo que podían los barcos al muro para enganchar sus escaleras a las fortificaciones y poder acceder con sus tropas a las almenas. Entonces entraba en acción la garra, que consistía en un brazo semejante a una grúa del cual pendía un enorme gancho de metal. Cuando se dejaba caer la garra sobre un barco enemigo el brazo se balancearía en sentido ascendente, levantando la proa del barco fuera del agua y provocando un ingreso del agua por lapopa. Esto inutilizaba los ingenios enemigos y causaba confusión, pero no era lo único que hacía: mediante un sistema de polea y cadenas, dejaba caer súbitamente el barco provocando una escoración que podía llevarlo al vuelco y al hundimiento.^13 15 36 Ha habido experimentos modernos con la finalidad de probar la viabilidad de la garra, y en un documental del año 2005 titulado Superarmas del mundo antiguo (Superweapons of the Ancient World) se construyó una versión de la garra y se concluyó que era un dispositivo factible.

En el entorno de Port-Royal

En otoño de 1654, Pascal sufrió un trastorno depresivo. Volvió a acercarse a Jacqueline, visitándola con frecuencia en el convento y se mudó a otro barrio para alejarse de sus amigos mundanos. Sin embargo siguió trabajando en cuestiones matemáticas y otros asuntos científicos. El 23 de noviembre, posiblemente después de un accidente con su carroza del que sin embargo no existen testimonios fidedignos, tuvo una experiencia religiosa de renacimiento que intentó registrar esa misma noche en una hoja de papel que aún se conserva, el así llamado Mémorial. La hoja, fechada "en el año de gracia de 1654, lunes 23 de noviembre, a partir de las diez y media de la noche aproximadamente hasta cerca de media hora después de la medianoche" comienza con la palabra "feu" (fuego) escrita en grandes letras mayúsculas, y relata una visión que ha experimentado. Incluye los fragmentos "¡Dios de Abraham, Dios de Isaac, Dios de Jacob, no el de los filósofos y los sabios!" y añade más adelante "El Dios de Jesucristo: sólo por los caminos que enseña el Evangelio se le puede hallar".⁷

Después se retiró por completo de la sociedad parisina para dedicarse por completo a su devoción. Sus únicas relaciones humanas pasaron a ser los «ermitaños» jansenistas (solitaires); se trataba de sabios y teólogos que se habían establecido en el entorno del convento Port-Royal des Champs y a los que visitaba con frecuencia. Alrededor de 1655 desarrolló aquí el diálogo legendario con su nuevo confesor A. Le Maître de Sacy (Conversation avec M. de Saci sur Épictète et Montaigne), en el que, entre los dos polos del escepticismo de Montaigne y la ética estoica de Epicteto, ya ofrece un esbozo de la antropología, que posteriormente desarrollaría en los Pensées.

La sanación, ocurrida en 1656, de su sobrina Marguerite Périer, que después de visitar Port Royal se había curado de un abceso en el ojo, contribuyó más a fortalecer la fe de Pascal. Al mismo tiempo, en docto diálogo con los solitaires, especialmente con Antoine Arnauld y Pierre Nicole, empezó a redactar escritos de motivación religiosa y teológica. A la par, como siempre, también se dedicaba a cuestiones prácticas, así por ejemplo en 1655 a la didáctica del aprendizaje de la lectura, para la escuela que mantenían los solitaires.

Blaise Pascal.

En el momento de su conversión (como indica el Mémorial), Pascal se vio implicado en una situación, en la que la devoción ortodoxa y el moralismo riguroso de los jansenistas se habían convertido en una molestia para los jesuitas, más relajados y conciliadores, pero también conscientes de su poder. Cuando en 1655 se desató abiertamente el conflicto, porque a Arnauld, en su calidad de jansenista, se lo expulsó de la facultad de teología de la Sorbonne en París, Pascal tomó partido y en 1656/57 redactó una serie de folletos satíricos polémicos anónimos. Estos tuvieron una resonancia explosiva y en 1657 incluso fueron publicados en Holanda en forma de libro, bajo el título de Lettres provinciales, ou Lettres de Louis de Montalte à un provincial de ses amis et aux R. R. PP. Jésuites sur la morale et la politique de ces pères (Cartas provincianas, o cartas de L. de M. a un provinciano amigo así como a los RR. PP. jesuitas sobre la moral y la política de estos padres). Se trata de dieciocho cartas supuestamente escritas por un personaje ficticio de nombre Montalte de viaje en París, de las que las primeras diez están dirigidas a un amigo ficticio en su provincia de origen, las siguientes seis a los padres jesuitas de París, mientras que las últimas dos se dirigen en especial al padre confesor del rey. En estas cartas, Montalte, primero en el papel de joven noble, ingenuo y no versado en teología, describe como los jesuitas le explican su teología de manera sabihonda y desdeñosa; después, aprendida la «lección», empieza a discutir con ellos, reduciendo al absurdo sus enseñanzas de manera aguda e hilarante. Pascal ridiculizó y atacó así la teología en cierto sentido amistosa y práctica, pero tendencialmente oportunista y muchas veces capciosa –la famosa casuística– de los jesuitas y desenmascara sus ansias de poder sumamente terrenales. Las Lettres provinciales tuvieron un éxito notorio y durable, aunque fueron prohibidas a partir de la número cinco, puestas en el índice al aparecer como libro y hasta quemadas por el verdugo en 1660, señalando a largo plazo el principio del fin de la omnipotencia jesuita, al menos en Francia. Por su claridad y precisión se las considera entre las obras maestras de la prosa francesa, que otorgaron a su autor un lugar entre los clásicos de la literatura francesa.

Fueron menos divulgados los cuatro escritos polémicos, con los que Pascal (junto a Arnauld y Nicole) intervino en 1658 en un conflicto entre párrocos parisinos de orientación jansenista y los jesuitas.

Lápida de Blaise Pascal en laiglesia de Saint-Étienne-du-Mont(París).

En lo inmediato, sin embargo, los jesuitas mantuvieron el control de la situación con la ayuda del Rey y del Papa, lo que ensombreció los siguientes años para Pascal. Porque mientras muchos de sus correligionarios cedían bajo la presión de las represalias que tomaba la autoridad o daban pasos tácticos, él permaneció indoblegable.

En medio de esta situación, en 1658 empezó a trabajar de manera más sistemática en una gran apologética de la religión cristiana. Con este fin había escrito unas primeras notas en 1656. Sus líneas principales se pueden encontrar en el escrito redactado en 1657 pero no terminado Écrits sur la grâce (Escritos sobre la Gracia), en el que explica la forma jansenista de la noción de gracia de San Agustín como término medio entre la noción casi fatalista de predestinación del calvinismo y la noción optimista de gracia de los jesuitas, asignándole a la libre voluntad del hombre el decidir sobre su salvación. Porque para Pascal rige: «Aquel que nos creó sin nuestro concurso, no puede salvarnos sin nuestra participación».

Aparte de su trabajo en los Pensées, volvió a emprender también estudios matemáticos. Así, en 1658, calculó la superficie de la cicloide con los métodos deCavalieri, así como el volumen del sólido de rotación que resulta de una rotación de la ciclode alrededor del eje de las x. Después de haber hallado la solución él mismo, organizó una competencia sobre el problema, lo que le significó recibir numerosas propuestas (insuficientes) así como desarrollar una intensa polémica con un descontento.

En 1659 apareció su escrito Traité des sinus des quarts de cercle (Tratado de los senos de los cuadrantes circulares). Cuando Gottfried Leibniz leyó esta obra en 1673 en París, recibió de ella un impulso decisivo para desarrollar el cálculo infinitesimal considerando el razonamiento específico por parte de Pascal, que Leibniz empleó de manera más general, interpretando el círculo de Pascal como círculo de curvatura en determinados puntos de una función o curva cualquiera. Leibniz dice que en ello había visto una luz que el propio autor no vio. De allí se origina el concepto de triángulo característico.⁸

Su salud deteriorada empeoró cada vez más deprisa en esos años, probablemente a consecuencia de su modo de vida extremadamente ascético, que lo debilitaba más. Por ejemplo, en 1659, no pudo trabajar durante numerosas semanas. A pesar de ello, en ese año fue miembro de un comité que trataba de poner en marcha una nueva traducción de la Biblia. En 1660 pasó varios meses de convalecencia en un palacete perteneciente a su hermana mayor y a su cuñado cerca de Clermont.

A principios de 1662, junto a su amigo Roannez, fundó una empresa de carrozas (Les carosses à cinq sous («Las carrozas de cincuenta centavos»), marcando el comienzo del transporte público local en París.

En agosto enfermó gravemente, hizo vender sus enseres domésticos donándolos para fines de caridad y murió, a la edad de solo 39 años, un año después de la muerte de su hermana Jacqueline, en casa de los Périer en París.

El período parisino

A partir de mayo de 1647 volvió a vivir con Jacqueline y poco después también con su padre, principalmente en París, donde contactó a los principales jansenistas, pero también continuó con sus investigaciones. Sus ideas no fueron bien recibidas por numerosos teólogos e investigadores, entre ellos Descartes con el que se reunió repetidas veces en París a fines de septiembre de 1647. Por ello a partir de entonces formuló sus especulaciones sobre el vacío y el éter de una forma más indirecta, particularmente en un tratado sobre la presión atmosférica, demostrando su dependencia de la altura del lugar en cuestión, por medio de experimentos que hizo realizar a su cuñado Périer en el Puy de Dome en 1648. También en 1648, en otro tratado, fundamentó la ley de los vasos comunicantes.

Pocos años antes (en 1644), Torricelli había publicado su experimento por el que el peso del aire de la atmósfera mantenía el mercurio en un tubo, con vacío en su parte superior, demostrando que el aire ejerce una presión debido a su peso. Pascal no estaba convencido de esa teoría, y seguía siendo partidario de la teoría del Horror vacui. Para confirmarlo, pidió a su cuñado que escalase el volcán Puy de Dôme hasta su cima, y se comprobó que el mercurio sube más en la base de la montaña que en su cima. Tras el experimento, Pascal abandonó la teoría del Horror vacui y se convirtió a la teoría de la causa mecanicista.⁴

Cuando, en la primavera de 1649, los desórdenes de la Fronda dificultaron la vida en París, los Pascal se refugiaron hasta otoño de 1650 en casa de los Périer en Auvergne.

En otoño de 1651 murió Pascal padre. Poco después y contraviniendo los deseos tanto del fallecido como también de Blaise, Jacqueline se incorporó al convento estrictamente jansenista de Port Royal en París.

Ahora, Pascal por primera vez dependía nada más que de sí mismo. Ya que, si bien no era rico, sí tenía una situación acomodada y era noble, comenzó a frecuentar la sociedad de París, trabando amistad con el joven duque de Roannez, con el que compartía el interés por la filosofía. Éste lo llevó de viaje en 1652, junto a algunos de sus amigos librepensadores, entre ellos Antoine Gombaud, conocido como el "caballero de Méré", oportunidad en la que Pascal se introdujo en la filosofía moderna, aprendiendo además el arte de las conversaciones sociales. Gracias a que frecuentaba el salón esteta de Madame de Sablé, se compenetró también con las «bellas letras» de su época.⁵ Incluso llegó brevemente a pensar en comprar un cargo y en casarse. Sin embargo, una obra que se le adjudicó por mucho tiempo, al amoldarse en cierto sentido a esta fase mundana de su vida, el anónimo Discours sur les passions de l’amour (Discurso acerca de las Pasiones del Amor), no es de su autoría.

En 1653 escribió un tratado sobre la presión atmosférica, en el que por primera vez en la historia de la ciencia se hace una descripción completa de la hidrostática.

Junto a sus nuevos conocidos, especialmente con el Chevalier de Méré, Pascal también tenía discusiones acerca del modo de ganar en los juegos de azar, un pasatiempos típicamente de nobles. Esto lo llevó en 1653 a dedicarse a la teoría de la probabilidad, estudiándola en 1654 en su intercambio epistolar con el juez de Toulouse y destacado matemáticoPierre de Fermat. Analizaron principalmente los juegos de dados. Al mismo tiempo, Pascal se ocupó de otros problemas matemáticos, publicando diversas obras en 1654: el Traité du triangle arithmétique acerca del llamado triángulo de Pascaly los coeficientes binomiales, en el que también por primera vez formuló explícitamente el principio de la demostración porinducción matemática,⁶ el Traité des ordres numériques acerca de los órdenes de los números y Combinaisons sobre combinaciones de números.